Current Projects
Convex Combination Belief Propagation
My dissertation research is advised by Pedro Felzenszwalb and we are interested in developing efficient algorithms for inference in probabilistic graphical models. Belief propagation is a widely used algorithm that computes marginal distributions of a graphical model. The problem is that when the graph contains a cycle, this algorithm may not converge or converge to the wrong limits.
In our current research, we are developing an alternative to the conventional algorithm called convex combination belief propagation. This message passing algorithm always converges regardless of the topology of the graph. At present, my advisor and I are working out the theory behind this algorithm which includes properties of the operator, providing a characterization of the limiting beliefs, and error analysis.
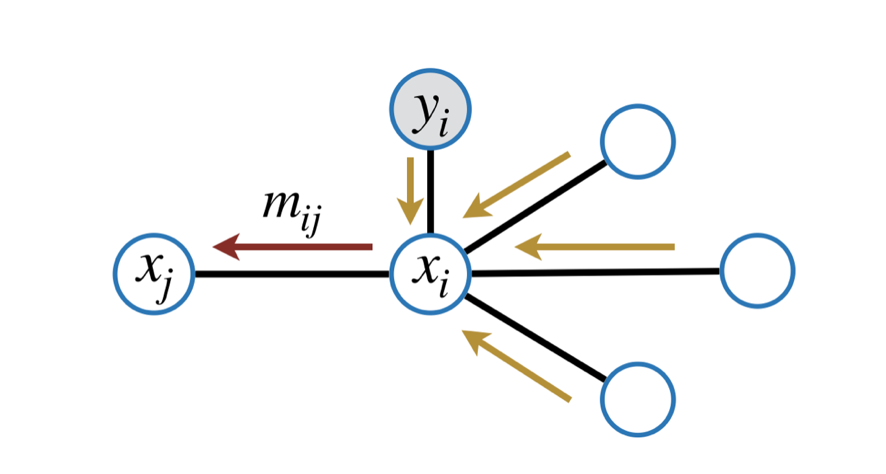
Illustration of Message Passing on a Graph
Approximate Inference in the QMR-DT Network
The QMR-DT network a Bayesian network that models complex relationship between diseases and symptoms as a factor graph. The objective is to assess the probability of a patient having a disease given an observation of symptoms. This is an inference task and the challenge is that this network has roughly 400 symptom and 3000 disease nodes. The scale and complexity of this network make exact inference computationally intractable. In this case, loopy belief is used to perform approximate inference, but this algorithm is unreliable due to the complexity of this network. The objective of this project is to generalize our weighted belief propagation algorithm to the case of a factor graph so that it can be applied to the QMR-DT network.

Example of a synthetic QMR-DT network
Past Projects
Cyclic Evasion in the Four Bug Problem
Choose any three points in the plane and suppose these point are bugs that walk away from each other at the same speed. The the triangle formed by these three points evolves as the bugs walk away from each other. It can be shown that the limiting shape is always an equilateral triangle. The goal of this project was to determine the limiting shape for any initial configuration formed by four bugs in the plane. We were able to show that when the initial configuration is convex, then the limiting shape is a parallelogram. When the initialization is non-convex, then the limiting shape is a line.
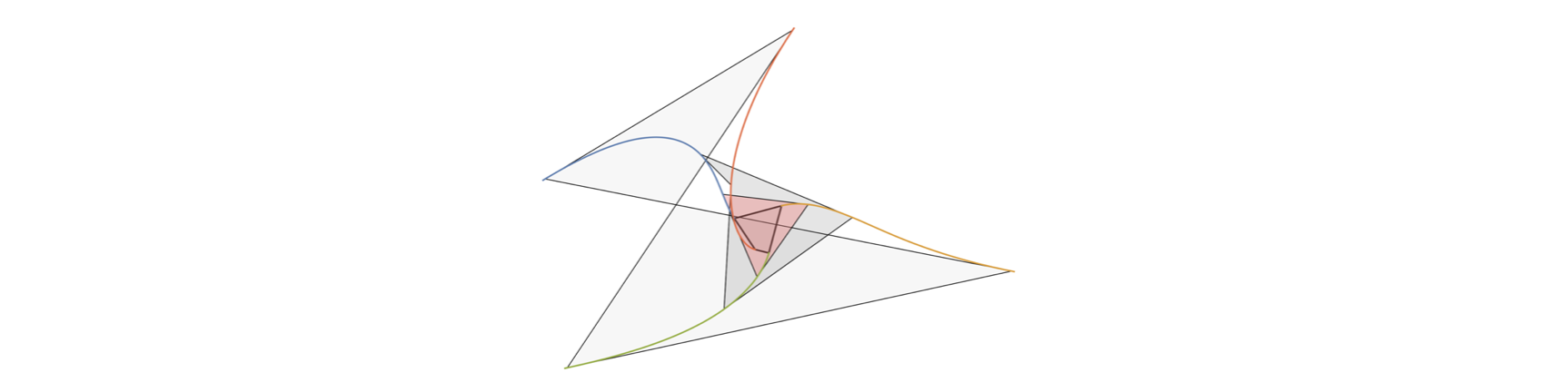
Trajectory of four bugs evading
Reassembly of Broken 3D Objects using Signature Curves
The goal of this project was to develop an algorithm that can be used to reassemble broken objects such as pottery, jigsaw puzzles, or in our case a broken ostrich egg. The crux of this algorithm is use compute the euclidean signature curve of the boundary of each piece, which is parametrized with respect to the basic differential invariants of a space curve up to euclidean transformations. Then the broken object can be reassembled by partitioning each piece into edges at the critical points of the signature curve. Then matching edges by comparing their corresponding signature curves.

Pieces of broken ostrich egg
Diagnosing Tumors from Mammograms using Signature Curves
The goal of this project was to develop an algorithm that can differentiate between benign and malignant breast tumors from a mammogram. One key difference between these types of tumors is the shape of their contour because benign tumors have a regular smooth shape whereas malignant tumors contain finger-like projections called spiculations. Our algorithm extracts features from the signature curve of each contour which is parametrized with respect to the differential invariants of a planar curve. Then the diagnose is determined by symmetry patterns that can be detected in the signature curve.
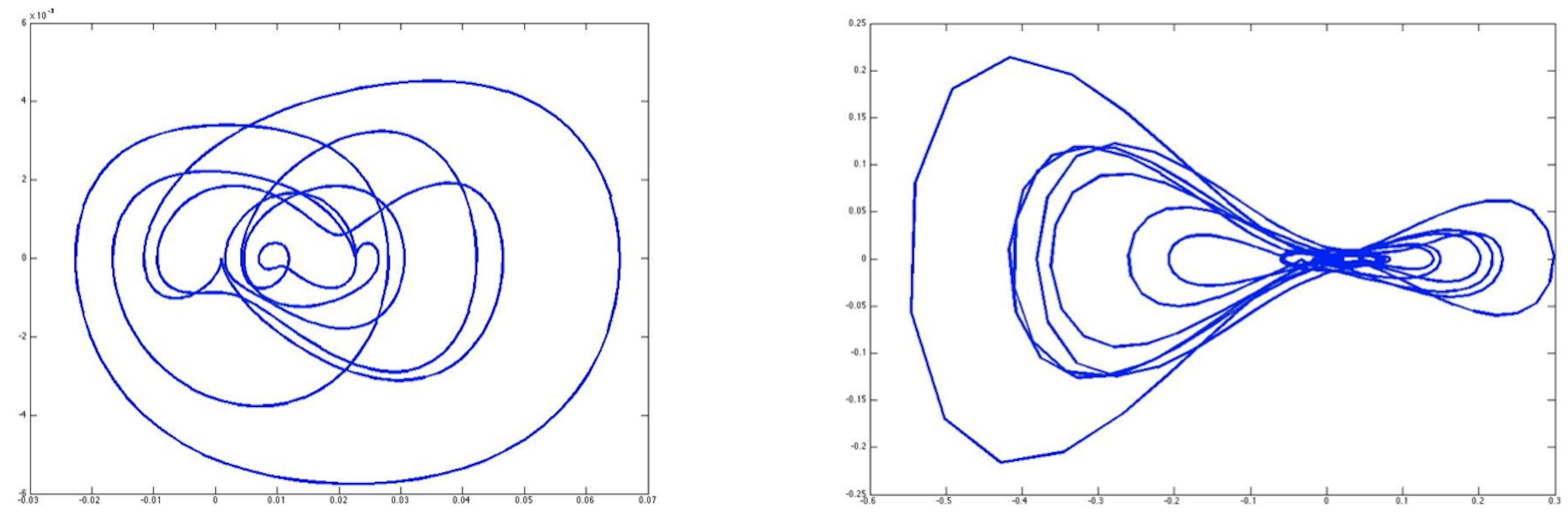
Signature curves of benign and malignant tumor contour, respectively